玻尔兹曼常数

对温度的重新定义：从水的三相点到玻尔兹曼常数

日常生活中，我们以相对的方式感知温度，比如“今天真冷，水管都冻住了！”或“孩子发烧了，39.5度”。这种方式依赖于比较和参照物。

热力学温度则提供了一种绝对的衡量标准。它量化了物体内部所有微观粒子平均拥有的总能量，包括动能和来自其他因素的能量。

早在18世纪，法国物理学家Guillaume Amontons就观察到，冷空气比热空气对液体的推力小。他由此推断存在一个“无限冷”的温度极限，空气在此温度下将失去所有弹性。这个概念深深吸引了许多物理学家。直到1848年，开尔文勋爵发表了《论绝对温标》，指出绝对零度对应着-273摄氏度。

为了纪念开尔文勋爵，国际单位制中采用了开尔文（K）作为热力学温度的单位。开尔文温标与摄氏温标使用相同的刻度间隔，但零点并非随意设定为水的冰点，而是设定为物质所能达到的最低温度。

○ 温度影响光的颜色：1850K的烛光呈红色，2800K的白炽灯发出暖黄光，而5000K的日光则呈现白色。| 图片来源：Wikipedia

水的三相点：曾经的定义基准

1954年起，1K被定义为水的三相点热力学温度273.16K的1/273.16。水的三相点是指水的三种状态（液态、固态和气态）处于平衡共存时的温度。在特定气压下，特定组成的水总是拥有相同的精确三相点温度：273.16K。

为了精确测量水的三相点温度，需要制造出水、冰和水蒸气稳定的共存状态。首先将干冰通入装置中央管道，使周围的水结冰。由于初始形成的冰存在缺陷和张力，需要静置一段时间使其达到稳定状态。测量前，将室温下的玻璃等设备插入中央管道，使最内层冰稍微融化，以便冰层自由转动。使用标准铂电阻温度计即可测量水的三相点温度。

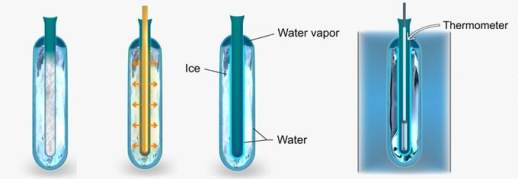
○ 测量水三相点温度的装置示意图。| 图片来源：NIST

仅凭水的三相点难以准确推断更广温度范围的数值。还需要其他参考点进行校准，例如金的凝固点（1337.33 K）和氧的三相点（54.3584 K）。

更重要的是，测量水三相点需要使用特定组成的水，对氢和氧同位素比例有着严格要求：每摩尔氢原子中需包含0.00015576摩尔的氘，每摩尔氧原子中需包含0.0003799摩尔的氧-17和0.0020052摩尔的氧-18。

○ 用于测量水三相点的水样需满足严格的同位素组成标准。| 图片来源：NIST

由于难以制备出完全相同组成的水，不同设备对热力学温度的测量结果 inevitably exhibit slight discrepancies. 是否存在更优的方式来定义热力学温度？

玻尔兹曼常数：全新的定义基石

2018年11月16日，第26届国际计量大会重新定义了1K：

1.380649×10^-23 J / k_B

其中k_B代表玻尔兹曼常数，其值为1.380649 × 10^-23 J·K^-1（焦耳每开尔文）。

玻尔兹曼常数将物质的动能（E）与其温度（T）直接联系起来：E=k_BT。这个以统计力学先驱之一——奥地利物理学家路德维格·玻尔兹曼命名的常数，是热力学中不可或缺的工具。

热力学温度描述了原子和亚原子粒子（例如铁块中的原子或房间里的空气分子）的平均能量，以绝对零度以上的开尔文数表示。

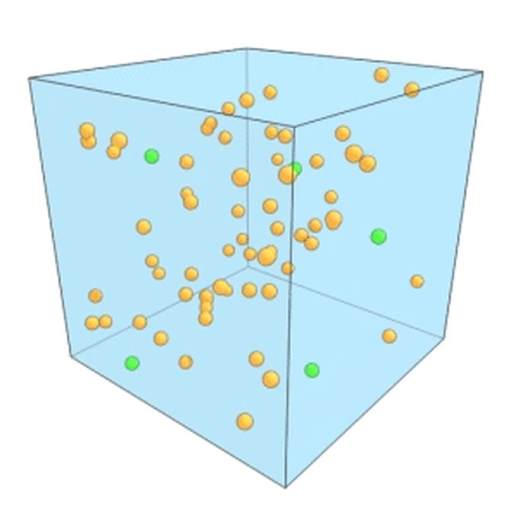
○ 平动是物体动能的主要形式：气体中的原子和分子不断进行着无规则的直线运动，并与彼此以及容器壁发生碰撞。| 图片来源：Sean Kelley/NIST

大多数物体的动能主要体现为平动能，即物体在空间中平行移动所具有的能量。气体中的原子和分子沿着各个方向飞驰，相互碰撞，并反弹容器壁。虽然单个粒子速度各不相同，但在特定温度下，大量粒子的速度分布遵循麦克斯韦-玻尔兹曼分布。这意味着大部分粒子的速度（能量）都集中在特定区间内。

热运动与玻尔兹曼常数

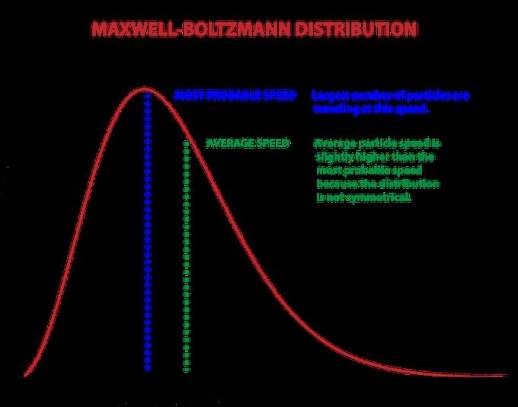
○ 粒子的速度和数量分布遵循麦克斯韦-玻尔兹曼分布。| 图片来源：Curt Suplee/NIST

物质的温度与其内部粒子的运动息息相关。对于气体而言，粒子的运动速度和数量分布遵循麦克斯韦-玻尔兹曼分布。但在固体中，原子受化学键束缚，无法自由移动。它们的动能以集体运动的形式存在，被称为声子。热能还可以通过自由电子在固体中传递。