100以内的素数 100以内的质数有哪几个
数学学科的兴衰往往与历史背景息息相关,鲜有始终如一的热门领域。数论便是这其中的例外,作为贯穿数学发展史的学科,数论的魅力历久弥新。

数论永恒的主题——素数
数论的核心是探究整数的性质,而素数无疑是最引人入胜的一类。尽管素数的实际应用并不多见,但它对数学家的吸引力却从未减弱。也许正是这种纯粹的探索才体现了数学研究的真正意义。

数学巨匠高斯
从欧几里得、阿基米德、斐波那契到文艺复兴时期的数学大师们,几乎所有伟大的数学家都对素数倾注了热情。而高斯,这位数学界的天才,更是对素数着了迷,并从少年时代便开始了深入的研究,取得了令人瞩目的成果。
素数研究并非投入时间和人力便能轻易取得进展,它与现代科研有着显著不同。数学史就是一部壮丽的素数研究史,更令人惊叹的是,许多看似简单的素数问题至今仍未得到解决。比如,是否存在无穷多组间隔为2的素数对?任意一个大偶数是否都是两个素数的和?
高斯在1792年便开始着手研究一个关于素数的重要问题。
一个自然数 N 以内的素数到底有多少个?
这个问题相较于直接寻找素数公式而言,显得更为温和,也正是这种温和使得它得以取得丰硕的成果。

纳皮尔与对数表
1792年,年仅 15 岁的 高斯,其数学天赋已初露锋芒。他拥有一本纳皮尔编著的对数表,这是一本内容枯燥的工具书,但其末页却藏有一个彩蛋,一张罗列了某个范围内所有素数的素数表,方便人们进行素数研究。高斯痴迷于素数,他基于这张素数表,统计了其中的规律,计算了不同范围内的素数个数。
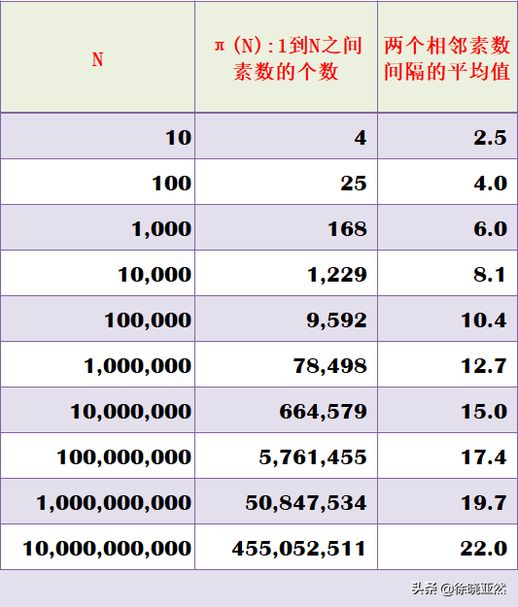
100 亿以内素数个数统计
事实上,这张表是否为高斯本人所作存在争议。在 18 世纪末,要获得 100 亿以内的所有素数,难度相当大。但即使这张表是后人编造的,也无法掩盖高斯伟大成就的光芒。
N 代表某个具体的自然数,π(N) 代表小于等于 N 的所有素数个数,最后一列则是“相邻素数间隔的平均值”。要注意的是,最后一列数据的意义在于,平均需要数过多少个自然数才能遇到一个素数。换句话说,在 1000 以内,素数占 1/6,而在 100 亿以内,素数大约占 1/22。这个通过统计得出的规律非常重要,高斯对于素数个数的猜测正是基于这些数据。
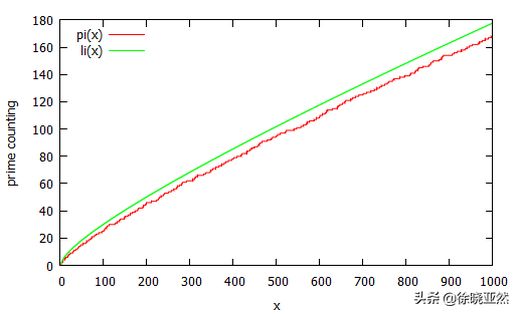
Li(x) 与真实 π(x) 的差距
观察表格,N 以 10 倍的速率增长,而相邻素数间隔的平均值却并非指数增长,甚至基本稳定在一个数值附近。这与我们对素数分布的直观感受相符。我们知道素数是无限多的,随着数值的增大,素数之间的距离会越来越大,分布也会越来越稀疏,但我们没想到素数占整个自然数的概率竟会稳定在一个基本值上。
分析最后一列数据,相邻两行数值的差大约为 2.3。如果我们将 N 作为自变量,最后一列的间隔平均值 L 作为未知量,构成一个函数,那么这个函数将会满足一个性质:N 增加 10 倍,L 始终增加 2.3。什么样的函数会满足这样的要求呢?答案是对数函数。命运的巧合,纳皮尔这位对数大师的著作冥冥之中引导着年轻的高斯走上了正确的道路。
高斯由此猜测,任意取一个自然数的概率应该是 1/logN,这里 log 的底数不确定,并不一定是 10。高斯表格中的自变量 N 以 10 倍递增,只是便于统计,实际上,即使用 7 倍增速、3 倍增速,也能得到类似结论。高斯只是猜测这两个关系之间应该是对数函数的关系。
既然猜测了素数的概率公式,自然可以进一步推测任意 N 以内的素数个数。
假设高斯拥有无限的计算能力,不再让 N 以 10 倍递增,而是让 N 一個一個加上去,再统计对应的数据。如果任意 N 以内的素数个数都满足上面的猜测公式,那么就可以得到一个估计公式:
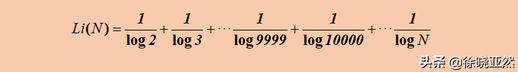
高斯推测的素数个数公式
上面的式子实际上是定积分的定义展开式,为了简化表示,可以写成一个积分:
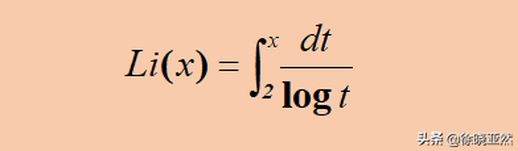
素数分布规律一直是数学家们研究的重点。高斯通过观察大量数据,提出了著名的素数定理,这个定理用一个函数来估计小于某个数的素数个数。
高斯的素数定理用积分形式表示,它表明:随着数越来越大,小于这个数的素数个数近似等于该数除以它的自然对数。
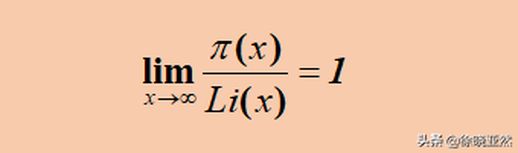
这个定理描述了素数在自然数域中的分布特点,但高斯并没有给出严格的数学证明。
为了验证素数定理的准确性,人们用表格来对比实际素数个数和素数定理估算的结果。
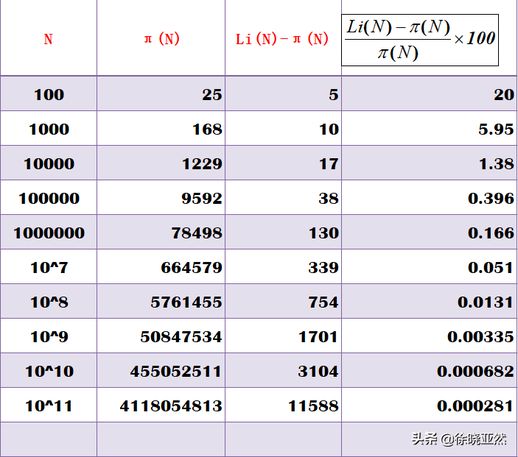
从表格中可以看出,随着数字的增大,素数定理估算的结果与实际素数个数的差距越来越小,验证了该定理的正确性。

高斯素数定理的证明经历了漫长的时间。黎曼在研究ζ函数时,提出了一个关于ζ函数零点的猜想,这个猜想与素数定理的证明密切相关。

19世纪末,数学家哈达玛和普森证明了黎曼猜想中非平凡零点都位于某个特定区域内,这也为素数定理的证明奠定了基础。

更令人惊奇的是,在1949年,塞尔伯格和埃尔德什给出了素数定理的初等证明,他们没有使用ζ函数,甚至没有用到微积分,仅利用一些基本的数学工具,就成功地证明了这个重要定理。
这个故事告诉我们,很多看似复杂的问题可能存在着简单的解决方法,而找到这种方法本身就需要非凡的智慧和努力。
高斯在年轻时就能够通过观察数据,推理出素数定理,这对数学界是一个巨大的贡献,也展现了他非凡的洞察力。
