十进制256转二进制 十进制25625转换为二进制

本文将详细讲解十进制数转换为二进制和十六进制数的方法。

方法一：除N取余，逆序排列

该方法的核心是：用目标进制的基数（二进制为2，十六进制为16）不断除十进制数，将每次得到的余数按逆序排列，即得到目标进制数的结果。

例1：K 200＝B？

用2不断除200，直到商为0，并记录每次得到的余数：

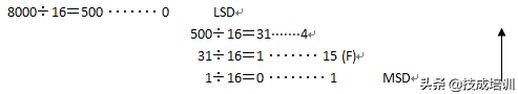
将余数按逆序排列，即可得到200的二进制表示：

K200＝B 1100 1000

例2：K 8000＝H？

用16不断除8000，直到商为0，并记录每次得到的余数：

将余数按逆序排列，即可得到8000的十六进制表示：

K8000＝H 1F40

方法二：找大位，定高位，依次除权，取商用余

该方法的核心是：找到目标进制数的位权值范围，并从高位开始依次除权，将商和余数作为目标进制数的对应位。

需要确定目标进制的位权值范围。位权值是指每个数位所代表的数值大小。例如：二进制的位权值分别是2⁰, 2¹, 2²...，十六进制的位权值分别是16⁰, 16¹, 16²...

找到一个大于十进制数的最小位权值，作为大位；找到一个小于十进制数的最大位权值，作为高位。 必须满足：大位>十进制数>高位

然后，从高位开始，用目标进制的基数不断除十进制数，得到商和余数。商作为对应位的数值，余数作为下一位的初始值，继续进行除法操作。

例1：K 200＝B？

找到二进制的位权值范围：
(大位) 256>200>128 (高位)

从高位128开始进行除法操作：

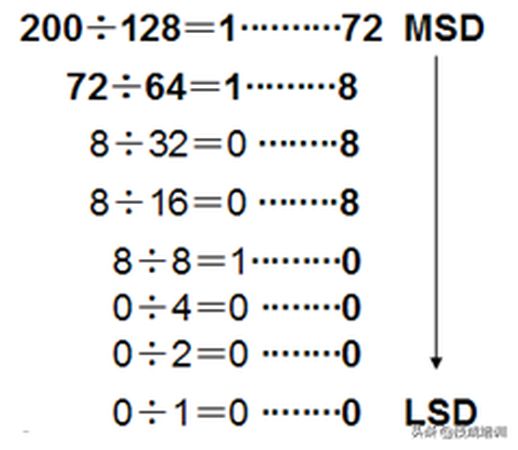
K200＝B 1100 1000

例2：K 8000＝H？

找到十六进制的位权值范围：
(大位) 65536>8000>4096 (高位)

从高位4096开始进行除法操作：

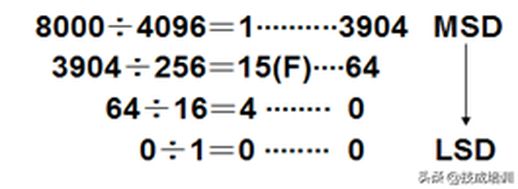
K8000＝H 1F40

需要注意的是，如果除法操作后，得到的商大于9，则需要用十六进制数A,B,C,D,E,F表示。

希望本文能够帮您更好地理解十进制数转换为二进制和十六进制数的方法。