奇函数的性质 奇函数的性质f 0=0

I. 引言

除了单调性，函数的本质特性包括奇偶性。让我们探索这一有趣的概念。

II. 奇偶性

函数的奇偶性可以分为奇函数和偶函数。

奇函数：

对于奇函数，任何变量 x，函数值满足 f(x) = -f(-x)。

偶函数：

对于偶函数，任何变量 x，函数值满足 f(x) = f(-x)。

III. 数学定义

奇函数：定义域中任意 x 满足 f(x) = -f(-x)

偶函数：定义域中任意 x 满足 f(x) = f(-x)

IV. 特征

1. 定义域关于原点对称：这是判断奇偶性的前提条件。

2. 函数图像：偶函数关于 y 轴对称；奇函数关于原点对称。

3. 原点值：奇函数在原点处的函数值为 0。

4. 同时为奇偶函数：高中阶段仅有 f(x) = 0（定义域为 R 或关于原点对称）满足此条件。

V. 常见奇偶函数

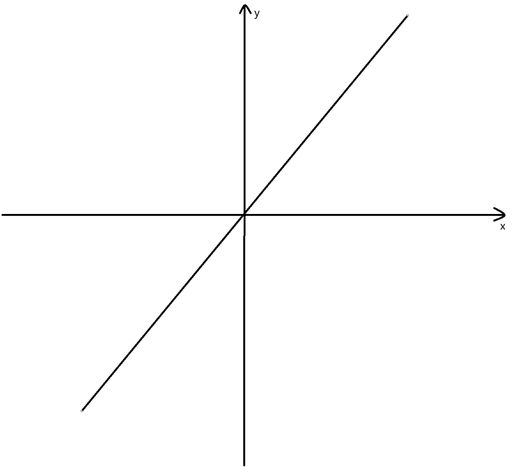
y = 2x

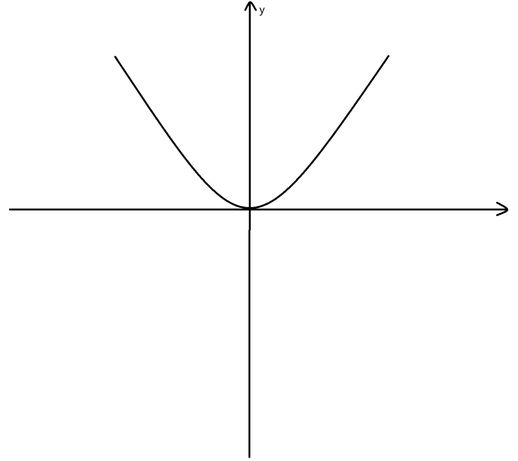
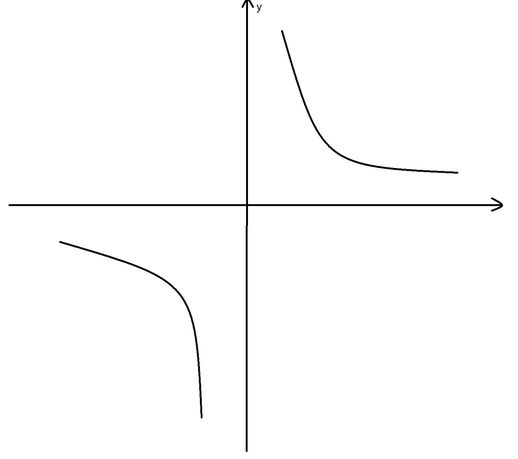
这些是常见奇偶函数，后续将不断补充和更新。

备注：

如有疑问或寻求解题经验，欢迎留言。关注、关注、关注！