什么是虚数 数学中什么叫虚数

数学源自实践，伴随其发展，其范围超出了人类的想象。虚数便是数学演变历程中的一个典型范例，时至今日，仍有许多人对虚数的概念感到困惑。本文将为您揭示虚数并不虚奥的本质。

设有一片边长为5米的正方形土地，现需将其扩展至39平方米，且仍保持正方形形状。这个简单的初中数学题要求我们求解方程（5+x）^2=25+39的根。所得结果为x=3或x=-13。根据题意，x=3是可行解，因为边长不能为负，因此-13为无效解。

如果前面的例子尚可理解，那么下面的方程似乎难以接受：x^2+2x+2=0。为了求解x，我们对方程进行变换：(x+1)^2=-1。显然，在实数范围内，该方程无解。什么样的数平方出来会是负数呢？

这种平方后产生负数的方程曾一度令数学家们百思不得其解。莱布尼兹就认为，这是数学分析中的异常，在现实世界中不存在，因此将这类数称为“虚数”。

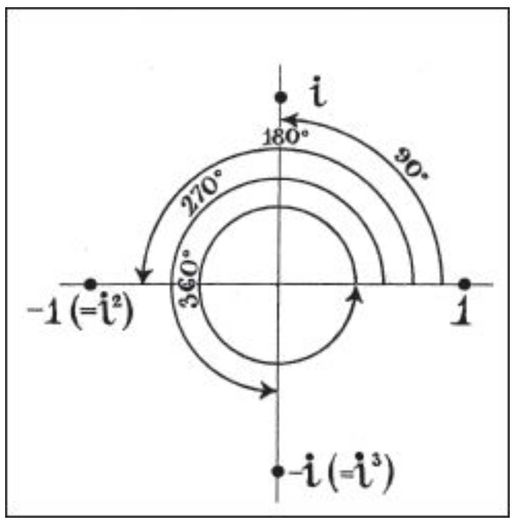
如今，我们已知-1的平方根为i，让我们探究一下i的特性。考虑一条数轴上的实数，1、2、3……，如果乘以-1，得到-1、-2、-3……。这些数相当于以原点为中心旋转180度。由于i^2=-1，这意味着，一个数乘以i两次就旋转了180度。

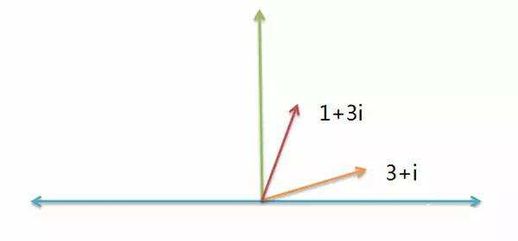
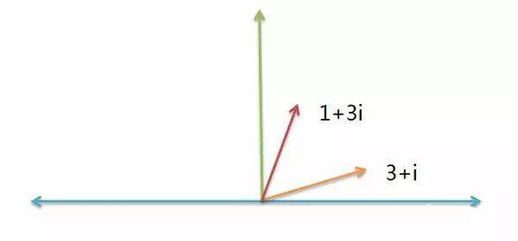
换言之，一个实数乘以i即意味着旋转了90度。我们将实数乘以i后的数称为纯虚数，它位于与实数轴垂直的虚数轴上。方程x^2-6x+25=0有两个根：x=3±4i，这两个根对应于由实数数轴和垂直于实数数轴的虚数轴构成的平面上的两个点。我们将实数+实数i这种形式的数称为复数。

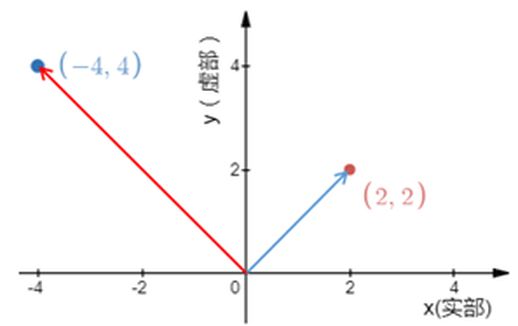
显然，复数具有超越仅有正负两个方向的实数的特点，它是一个能够描述平面上所有点方向的更广义上的数。虚数i的意义在于，它与实数共同构建了一个向量空间，其中复数描述了该空间中点到原点的距离及其相对于实数正方向的偏角。

对于复数z=a+bi，其到原点的距离为r=（a^2+b^2）^(1/2)，其偏角为θ，tanθ=b/a。r被称为z的绝对值，记作|z|，θ称为 z的辐角，记作arcz。

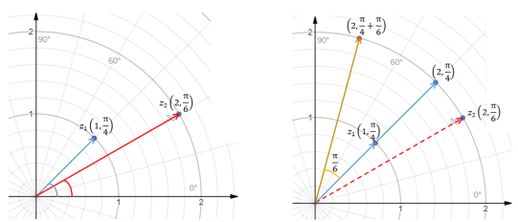
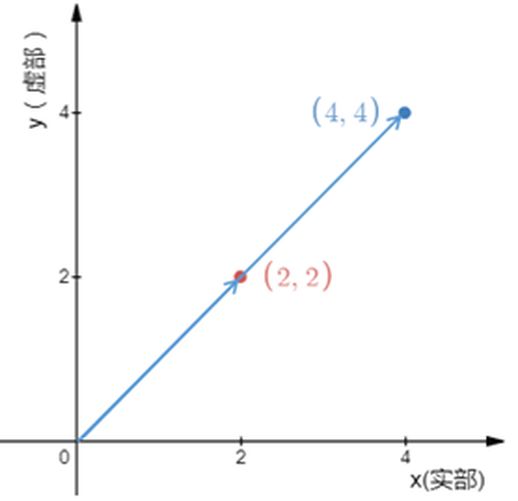
物理学中经常需要计算质点的位移。利用复数，这一过程变得十分简便。例如，某质点在t1时刻位于复平面上点r1=2+3i，在t2时刻位于r2=5+3i，求t1、t2时刻位移的变化Δr。这很简单，Δr=r2-r1=3。这意味着，在此段时间内，质点沿实数轴正方向移动了3个单位，而在虚数轴正方向的位置保持不变。

由于超出数学范畴，这里简要总结一下复数运算的物理意义。复数的加减法对应于沿实数轴和虚数轴的平移，而复数的乘除法对应于复数的伸缩和旋转。正是由于复数的这些性质，它被自然地应用于物理学中。

在GPS导航中，复数用于计算和描述交通工具的位置及其位置变化信息。由于复数既有大小（距离）又有辐角，因此也被广泛用于描述许多周期性变化运动，尤其是在电磁学中，并最终被应用于量子力学。

如今，复变函数是物理专业学生的基本计算技能，是物理系本科生的必修课。

虚数有着广泛的应用，本文仅作简要阐述。从数学角度来看，虚数拓展了数系的范围，为高次方程提供了有意义的解决方案，并拓展了几何问题的解题思路。在物理领域，虚数与实数共同构建了复数平面，用于描述空间中任何点的距离和方向。任何涉及距离和方向的物理量都可以用复数表示，这恰好是物理学探索的核心问题。

由此可见，虚数并非真正的“虚”，而是数学和物理学中不可或缺的工具。欢迎大家在下方留言区分享你们对虚数及其实际应用的看法。