滑轮组的机械效率 机械效率实验

利用滑轮组打捞物体

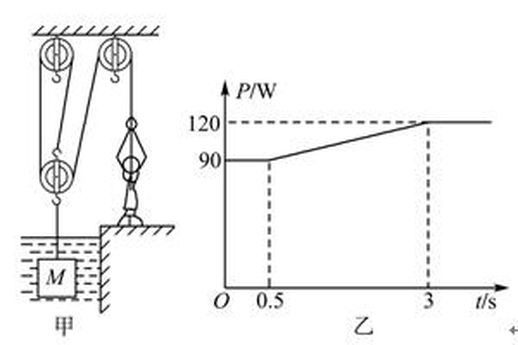
如下图所示，质量为60 kg的人利用滑轮组将密度为3.6 g/cm³的圆柱形物体M从水底吊起。绳子自由端以0.6 m/s的恒定速度向上移动。图乙为作用在绳子上的拉力功率P随时间t变化的图像。不计绳重、轮轴间摩擦、水的阻力及水位变化。（g取10 N/kg）求：

（1）人的重力；

（2）打捞前，物体M上表面受到的水的压强；

（3）物体出水后，滑轮组的机械效率。

解析
1. 人的重力
直接根据公式计算：

G_人 = m_人g = 60 kg × 10 N/kg = 600 N

2. 物体M上表面受到的水的压强
分析图乙可知，在0~0.5s内，拉力功率恒定，说明物体完全浸没在水中；在0.5~3s内，拉力功率逐渐增大，说明物体部分露出水面；3s后拉力功率再次保持恒定，说明物体完全离开水面。
由此可知，物体在水中上升的时间为0.5s，上升的高度为：

h = v_物t = (0.6 m/s ÷ 3) × 0.5 s = 0.1 m

则打捞前物体M上表面受到水的压强为：

p = ρ_水gh = 1.0×10³ kg/m³ × 10 N/kg × 0.1 m = 1000 Pa

3. 物体出水后，滑轮组的机械效率
由图乙可知，物体出水前拉力的功率P₁ = 90W，物体出水后拉力的功率P₂ = 120W。
根据公式P = Fv，可得物体出水前、后绳端的拉力分别为：

F₁ = P₁ / v = 90 W / 0.6 m/s = 150 N

F₂ = P₂ / v = 120 W / 0.6 m/s = 200 N

将物体和动滑轮看成一个整体进行受力分析，可以得到以下两个方程：
物体未出水时：3F₁ = G_物 + G_动 - F_浮 = 450 N
物体出水后： 3F₂ = G_物 + G_动 = 600 N
将上述两式联立，可得F_浮 = 150 N。
根据阿基米德原理可得物体的体积：

V = F_浮 / (ρ_水g) = 150 N / (1.0×10³ kg/m³ × 10 N/kg) = 0.015 m³

则物体的重力为：

G_物 = ρ_物Vg = 3.6×10³ kg/m³ × 0.015 m³ × 10 N/kg = 540 N

根据公式η = G_物 / (nF₂) 计算出物体出水后滑轮组的机械效率：

η = 540 N / (3 × 200 N) = 90%