回归方程公式怎么套的 回归方程相关系数r的计算公式

在高考中，线性回归方程的理解与应用逐渐成为考试的重点内容之一。这不仅考查学生对回归直线的求解能力，更注重统计知识在实际问题中的运用能力。考生需要掌握数据处理的基本方法，并能够在生活中的实际情境中灵活应用这些知识。

试题特点

1. 试题设计充分考虑考生的生活背景和城乡差异，体现了公平性原则。题干简单明了，语言自然易懂。

2. 试题内容与《考试大纲》和《考试说明》一致，考查学生对最小二乘法的理解，要求能够根据给出的线性回归方程系数公式构建线性回归方程。整体难度适中，旨在测试学生的基本素养。

随着教育改革的深入，线性回归方程在高考中的考查频率不断增加。早期此类题型较少，但如今已成为高中课程中的常见内容，突显了这一知识点的重要性，学生们应当给予充分重视。

在统计与概率的高考分析中，以下是几个典型例题：

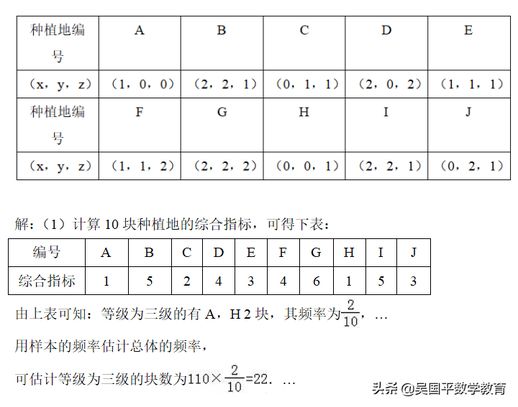
某县生产的“瓜州蜜瓜”有多个系列和品种，以其质脆汁多、香甜可口而闻名。蜜瓜的含糖量高达14%到19%，成为夏季消暑的优选。研究显示，蜜瓜的甜度与海拔高度、日照时长和温差之间存在显著的相关性。通过将甜度用x，日照时长用y，温差用z表示，研究人员对这三者进行了量化，0表示一般，1表示良好，2表示优质。综合指标w的计算公式为w=x+y+z。如果w≥4，则归为一级；2≤w≤3则为二级；0≤w≤1则为三级。今年来，周边省份也纷纷开始发展蜜瓜种植，研究团队随机抽取了10块蜜瓜种植地，以此了解不同地区的种植情况。

（1）在110块蜜瓜种植地中，估算出三级的蜜瓜种植地的数量。

（2）在样本中随机抽取两块等级为一级的蜜瓜种植地，求出这两块地综合指标w至少有一个为4的概率。

考点分析：

在计算中，需列举基本事件及事件发生的概率。

题干分析：

（1）通过计算10块种植地的综合指标，并列出相应表格，发现等级为三级的有A、H两块，频率为2/10，这样可以估算出三级种植地的总数。

（2）从等级为一级的地块（ω≥4）中，记录下B、D、F、G、I共5块，随机抽取两块，利用列举法可求出这两块地综合指标ω至少有一个为4的概率。

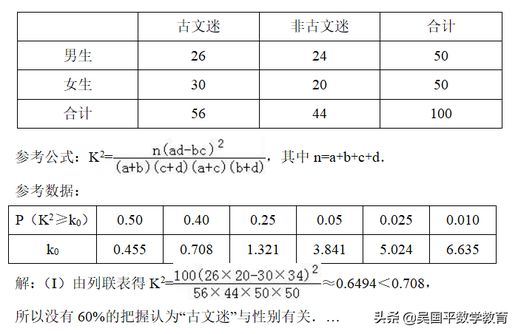
另一个相关例题为，某学校为了调查高三学生每天自主学习中国古典文学的时间，随机抽取了100名学生进行问卷，结果发现，学习时间超过3小时的学生称为“古文迷”，其他的则为“非古文迷”。根据收集到的数据，进行了如下分析：

（Ⅰ）能否以60%的把握判断“古文迷”与性别之间存在关联？

（Ⅱ）在女生中按分层抽样抽出5人，计算“古文迷”和“非古文迷”的人数。

（Ⅲ）从（Ⅱ）中选取的5人中随机抽取3人，记其中“古文迷”的人数为ξ，求出随机变量ξ的分布及其数学期望。

考点分析：

本题聚焦于线性回归方程的应用。

题干分析：

（Ⅰ）通过计算K²并与临界值比较可得出结论；

（Ⅱ）从调查中找出“古文迷”30人及“非古文迷”20人，按分层抽样抽取5人，进行进一步分析；

（Ⅲ）随机变量ξ的取值为1、2、3，需计算相应概率以求得分布列与期望。

在另一例题中，某公司推出新产品，计划在6个时段内进行试销，并对销售情况及顾客评价进行跟踪。试销期间共销售480件，通过数据分析发现产品的好评率为5/6，服务的好评率为0.75。发现销量与单价之间存在线性相关关系，具体数据如下：

考点分析：

本题同样涉及线性回归方程。

题干分析：

（1）根据题意构建2×2列联表，并利用公式求出K²的观测值，与参考表进行比较得出结论；

（2）计算样本的中心点坐标，并求出回归方程的系数，写出利润函数w的解析式，进而求出w（x）的最大值以及对应的x值。

通过对以上问题的深入分析，可以看出，线性回归与概率统计在实际应用中的重要性日益凸显。掌握这些知识不仅是高考的需要，更是