阿基米德螺线弧长求法 阿基米德螺线的曲率半径
本文将深入探讨几种常见的机械设计曲线及其方程,这些曲线在参数设计中应用广泛。通过对这些曲线的分析,设计师能够更高效地解决复杂的工程问题,摆脱传统的气缸堆砌方法。接下来,我们将详细介绍每种曲线的定义、特性以及相应的方程。
1、圆
1)标准形式的圆形
(1) 曲线图

(2) 方程
A、角坐标方程

此圆心位于O(0,0),半径为R。
B、极坐标方程
ρ=R(在极坐标系中,圆心O的极径为0)。
C、参数方程

(3) 定义与特性
圆的轨迹是与固定点等距的所有点的集合。
2)一般形式的圆形
(1) 曲线图

(2) 方程
A、直角坐标方程
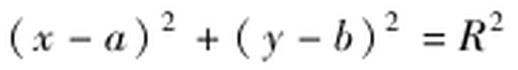
该圆心位于O'(a,b),半径为R。
B、极坐标方程

极坐标方程(圆心为O',半径R)。
C、参数方程
参数方程(半径R)。
(3) 定义与特性
同样地,与定点等距离的动点轨迹形成的圆。
2、椭圆
1)椭圆的曲线图
2)方程
A、直角坐标方程
B、极坐标方程
(极点在椭圆的中心O点)
C、参数方程
D、准线
3)定义与特性
椭圆的轨迹是动点P到两个焦点F1和F2的距离之和为常数的点的集合。
备注:
2a——长轴(A1A2)
2b——短轴(B1B2)
2c——焦距(F1F2)
e——离心率(e越大,椭圆越扁平)。
焦点F1和F2的坐标为F1(-c,0)和F2(c,0)。
焦点半径:r1=PF1,r2=PF2。
3、双曲线
1)曲线图
2)方程
(1) 直角坐标方程
(2) 极坐标方程
(极点在双曲线中心O点)
(3) 参数方程
(4) 准线
(5) 渐近线
3)定义与特性
动点P到两定点F1、F2(焦点)的距离之差为常数时,P点的轨迹即为双曲线。
备注:
(1) 2a——实轴,指双曲线两顶点之间的线段。
(2) 2b——虚轴,通常用以图示化。
(3) 2c——焦距。
(4) e——离心率,e越小,渐近线与x轴的夹角越小。
4、抛物线
1)曲线图
2)方程
(1) 直角坐标方程
(2) 极坐标方程
(3) 参数方程
(4) 准线
3)定义与特性
抛物线的轨迹是动点P到焦点F与准线l的距离相等。
备注:
离心率e=1,焦点和顶点的坐标为O(0,0)。
5、渐开线
1)曲线图
2)方程
(1) 极坐标方程
R——基圆半径,α——压力角。
(2) 参数方程
3)定义与特性
当一条直线沿一定圆作无滑滚动时,其轨迹即为渐开线,广泛应用于齿形设计等。
6、阿基米德螺线
1)曲线图
2)方程
极坐标方程:ρ=αθ。
3)定义与特性
动点沿着等速旋转的圆的半径作等速直线运动,形成阿基米德螺线,常用于凸轮设计。
7、对数螺线
1)曲线图
2)方程
极坐标方程:θ与ρ均为常数。
3)定义与特性
动点的运动方向始终与极径保持一定夹角,广泛应用于涡轮叶片等设计。
8、圆柱螺旋线
1)曲线图
2)方程
参数方程描述右旋和左旋的情况。
3)定义与特性
在圆柱面上,动点绕定轴回转并沿轴平移,形成圆柱螺旋线,常见于弹簧设计。
9、圆锥螺旋线
1)曲线图
2)方程
参数方程形式列出。
3)定义与特性
在圆锥面上,动点的轨迹形成圆锥螺旋线,其特性包括等螺距和切角等。
10、圆锥对数螺旋线
1)曲线图
2)方程
参数方程描述此曲线的特性。
3)定义与特性
此曲线具有不等螺距和定角切线特性。
11、外摆线
1)曲线图
2)方程
参数方程为主。
3)定义与特性
外摆线是由滚动圆在基圆外部滚动形成的轨迹。
12、内摆线
1)曲线图
2)方程
参数方程概述。
3)定义与特性
内摆线的轨迹来源于滚动圆在基圆内部的相切滚动。
13、平摆线
1)曲线图
<p style="text
2)方程
参数方程为:
x=bt - lsin(t)
y=b - lcos(t)
3)定义与特性
平摆线的轨迹是一个定圆沿一条定直线滚动时,圆周上一点的轨迹。这种曲线的特性使其在机械设计中具有重要的应用。
14、悬链线
1)曲线图
2)方程
直角坐标方程如下:
——常数,即距离。在顶点附近近似于抛物线。
3)定义与特性
悬链线是一种由重力作用下形成的曲线,两端悬吊的密度均匀柔软绳索的自然形态。它的特性在工程设计中尤为重要,尤其是在桥梁和悬挂结构中。
随着对这些常用曲线的理解,设计师们能够更灵活地应用这些数学工具,在机械设计中提升创意和效率。这些曲线的定义、方程以及特性,为设计提供了坚实的理论基础,推动了工程技术的发展。
本文还将继续探讨常用几何体的面积、体积及重心位置等相关内容,敬请期待。通过深入的学习与研究,这些知识将帮助设计师更好地掌握机械设计的核心原理,开创更为创新的设计方案。
掌握各种曲线及其方程的特性,是机械设计师在实际工作中不可或缺的技能。借助这些工具,可以在复杂的设计任务中做出更为精准和高效的决策,推动整个工程行业的进步。
