万有引力定律 万有引力圆周运动公式

在科学史上，万有引力定律的提出不仅改变了人类对宇宙的理解，还为后续的天文探索奠定了坚实的理论基础。这一伟大的发现源于牛顿在1687年发表的《自然哲学的数学原理》。从定律的提出到实际测量地球质量的实现，科学家们经历了漫长的111年，期间涌现出许多杰出的人物和重要的理论。

许多人可能会好奇，为什么苹果会从树上落下，而不是朝上飞去？地球虽然以每秒460米的速度自转，为什么我们没有被甩入太空？这些在现代看来简单的问题，在17世纪却没有明确的答案。在这个时期，约翰尼斯·开普勒在他的老师第谷·布拉赫的研究基础上，经过无数次的观察和计算，终于提出了著名的开普勒三定律，为行星运动提供了理论框架。

开普勒的三大定律概括如下：

第一定律：行星绕太阳的轨道是椭圆，太阳位于椭圆的一个焦点上。

第二定律：行星与太阳之间的连线在相等时间内扫过的面积相等。

第三定律：行星轨道半长轴的三次方与公转周期的平方比值是一个常数。

尽管开普勒的定律为天体运动提供了新视角，但他本人对这一现象的原因仍感到困惑。他曾提出太阳磁力流的假说，认为太阳系的行星受太阳的磁力控制。与此笛卡尔也提出了宇宙中充满不可见流体的观点，认为流体的运动形成旋涡，使得行星得以环绕太阳旋转。这些理论并未能充分解释行星运动的奥秘。

随着时间的推移，胡克、雷恩和哈雷等科学家对引力的理解逐渐深入。他们意识到地球上物体受到的重力和宇宙中行星的运动受到的是同一种力量，甚至提出了引力与距离平方成反比的理论。真正完成这一理论体系的人是牛顿，他利用微积分和开普勒的定律，最终在1687年提出了万有引力定律。这一理论明确了任何物体之间都存在引力，且引力的大小与物体的质量乘积成正比，与两物体之间距离的平方成反比。

万有引力定律在牛顿的著作中首次系统性地被阐述，尽管这一伟大的理论被提出，但万有引力常数G的具体数值却无法从理论中推导出来，依然需要依靠实验进行测量。由于引力的强度极弱，科学家们在接下来的一个世纪里仍未能准确测定其值。

这一突破直到1798年，英国科学家亨利·卡文迪许才得以实现。他受到约翰·米歇尔使用扭秤测量磁力的启发，改进了实验方法。卡文迪许的实验设计巧妙，他悬挂了一根金属哑铃，利用两个固定的大铅球吸引小铅球，从而使得悬挂的金属丝发生微小的扭转。这个过程中的力矩平衡，让他能够通过计算得出万有引力常数G的值。

实验并非易事。由于引力的微弱，金属丝的扭转几乎无法用肉眼观察。卡文迪许巧妙地在金属丝上挂上小反光镜，通过光线的反射来测量扭转角度，从而提高了实验的精确度。除了对实验环境的严格控制外，卡文迪许还需多次反复实验以确保结果的可靠性。经过几年的努力，他最终在快70岁时成功测得引力常数的值为6.754×10^-11 N·m²/kg²，现代值为6.67408×10^-11 N·m²/kg²。这一成就使他获得了“测量地球质量的第一人”的美誉，成功推导出地球的质量约为60万亿亿吨。

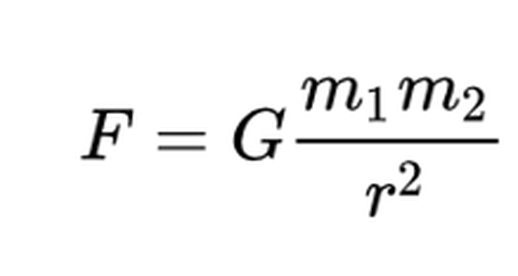
万有引力的发现和测量是科学史上的重要里程碑，它不仅推动了物理学的发展，也为后来的太空探索打下了基础。牛顿的理论使得人类对宇宙的认知迈上了一个新的台阶，开启了科学家们对引力本质和宇宙结构的深入研究。