球的体积公式怎么算 球体的半径怎么算
在中国悠久的历史中,古代数学以其独特的方式承载着文明的智慧。从结绳记事到文字记录,古人们早已在数字与几何中探索出深邃的知识。
西安半坡村出土的陶器上,留下了各种几何图形的印记,显示出人们在5000到6000年前就已经掌握了圆与方的绘制技巧。

半坡陶符光影图
尽管如此,许多人对古代中国的数学成就并不十分看重,认为它最多只能算作算术,而与以逻辑推理为基础的西方数学有所不同。
例如,勾股定理在中国的发现虽早于西方,但由于缺乏证明,直到西方才得以流传。而如今,勾股定理仍被称为“毕达哥拉斯定理”,因为毕达哥拉斯是第一个为其提供证明的人。
其实,中国的数学同样辉煌。例如,我们现在所熟知的球的体积公式,就是由古代中国数学家通过巧妙的推导得出的。
在这其中,《九章算术》、刘徽和祖暅三者的智慧闪耀着光芒,让我们一起探索这些古代数学的精彩瞬间。

在《九章算术》中,“少广”章专门探讨了“开方术”和“开立方术”。其中的一个问题询问:“已知体积为00尺的球,求该球的直径。”这个问题的解法在“开立圆术”中明确指出:“将体积乘以16,再除以9,最后开立方,就可得出球的直径。”
《九章》认为正方体的体积与其内切球的体积之比为16:9。虽然这一比例在现代数学看来并不精确,但在当时已经相当出色。这个比率的来源与古代对“方”和“圆”的理解密切相关。根据《周髀算经》的记载,古人将圆周率取为3,因此得出正方形与其内切圆的面积之比为4:3。
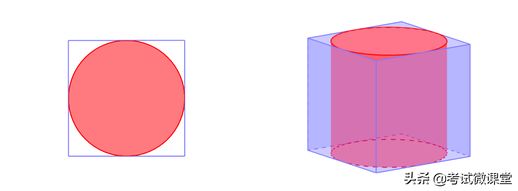
进而推导出正方体与圆柱体的比例,以及圆柱体与球体的比例,最终得出正方体与球体的比例为16:9。尽管这个结论并不够精确,古人的智慧依然令人敬佩,因为他们在数学推导中灵活运用了几何概念。
刘徽,这位魏晋时期的杰出数学家,在为《九章算术》注释时,发现了上述推导中的错误,认为“圆柱体与球体的比例应为4:3”是错误的。他将3替换为π,推导出“圆柱体与球体的比例为4:π”。利用现代数学知识可得,设球的半径为r,圆柱的高为2r,则圆柱的体积为2πr³,而球的体积为4/3πr³,这表明比例确实存在偏差。

刘徽面对问题,选择从正方体出发,构想出一种名为“
牟合方盖
”的几何体。它由一个正方体内切的圆柱体构成,两个相同的面合在一起,形成一个复杂的几何体。

看似简单的“牟合方盖”这一创举,彰显了刘徽的非凡才智。值得注意的是,圆周率的计算与“割圆术”密切相关,而这项技术正是刘徽的发明,后来的祖冲之虽将圆周率计算得更为精确,但刘徽无疑是这一理论的奠基者。牛顿曾说:“我之所以能看得更远,是因为我站在巨人的肩膀上。”而在祖冲之也可以说:“每个人都有值得仰望的巨人。”
刘徽的“牟合方盖”不仅包含了正方体的内切问题,还保持了二者的切线关系。若用水平面截取该方盖,所得到的正方形与内切圆的面积比例为4:π。最终,问题的核心便在于如何计算“牟合方盖”的体积,解决这一难题后,球的体积便能迎刃而解。
剧情迎来了转折,刘徽说:“我无法解决此事,谁能担当这个重任?”
当时的社会背景下,即使是刘徽这样的数学大家也难以找到解决方案。球的体积计算因此暂时搁置。接下来,让我们期待另一个数学巨匠的到来。
祖暅,南北朝时期的杰出数学家,祖冲之的儿子。他与父亲一样,才华横溢,父子齐心,为中国数学发展注入了新的活力。
祖暅深知,要想有所成就,必须依靠前人的智慧。他的父亲利用刘徽的“割圆术”成功地计算出圆周率,声名远播。而祖暅则选择了从刘徽的“牟合方盖”入手,继续开辟新的数学领域。
当祖暅思考如何求得“牟合方盖”的体积时,他意识到,必须找到一种巧妙的方法。在某个平常的日子,祖暅在看着两摞铜钱时,偶然发现这两摞铜钱的体积总是相等。这个简单的观察让他思考为什么会如此。
祖暅意识到,两个几何体在任意截面处的面积相同,因此体积也必然相等。这一发现促成了“祖暅原理”的形成:
若两个几何体在任意截面处的面积相等,则它们的体积相等。
这个原理在西方要等到一千年后,才由意大利数学家卡瓦列利提出。
有了“祖暅原理”,祖暅不再需要直接计算“牟合方盖”的体积,而是寻找一个简单易求且满足“幂势既同”的几何体。他的想法让人耳目一新。
经过深思熟虑,祖暅找到了一个简单的几何体,即将“牟合方盖”切割成8个“小方盖”。通过巧妙的切割方法,这个小方盖的体积与“牟合方盖”的体积一致。
通过这一过程,祖暅将“小方盖”的体积进行了详细的计算。在这一过程中,他虽然没有现代数学符号,但其智力和创造力展现了惊人的能力。
将“小方盖”放置在一个边长为r的正方体中,接下来通过图示进行计算,找到与“小方盖剩余”相同的几何体,最终利用刘徽的体积比例,得出球的体积公式为4/3πr³。这一公式的诞生,标志着中国古代数学的伟大成就。
这一公式不仅在千年后得以验证,且其推导方法为后来的数学问题提供了清晰的路径。中国古代数学虽与古希腊的数学体系迥然不同,但同样丰富多彩,充满了实践智慧。
中国古代数学以其独特的风格和深厚的文化底蕴,为后世的发展打下了坚实的基础。许多算法如十进位制、盈不足术等,曾经传入印度和阿拉伯,再由此传播至欧洲,对全球数学发展产生了深远的影响。
