直线与圆的位置关系 直线与圆的方程知识点总结

直线与圆的关系是初中数学中一个重要的知识点，尽管中考对此的要求不算严格，但掌握其基本概念和性质对于学生的数学思维发展至关重要。通过深入理解这一主题，学生能够在数学学习中获得更深的启发与思考。

直线与圆的位置关系可以从两个主要角度进行分析。一个是方程法，通过联立圆和直线的方程，并使用判别式来判断位置关系；另一个是几何法，比较圆心到直线的距离与圆的半径大小。在中考中，通常采用几何法来进行判断。

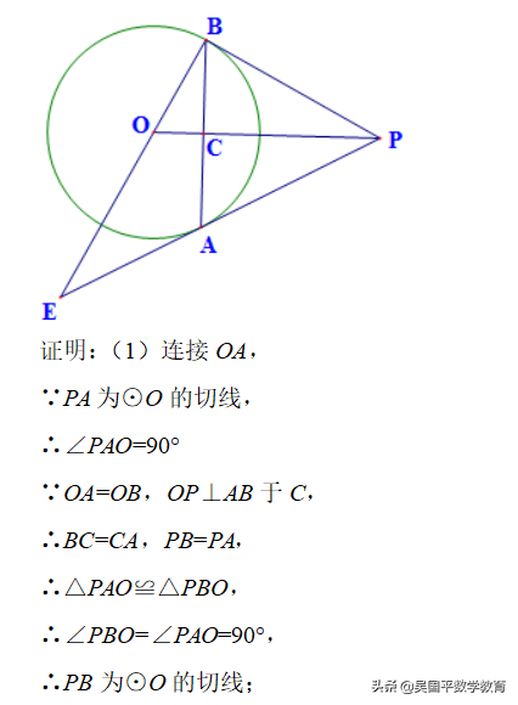
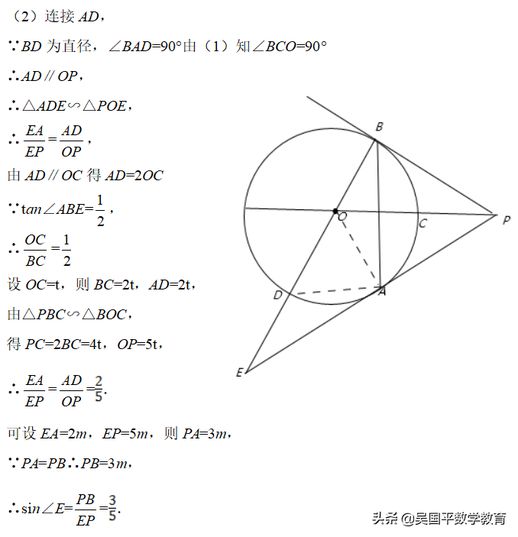
为了解决相关问题，理解圆心到直线的距离和半径之间的关系是关键。例如，考虑一条切线PA与圆⊙O相切，切点为A。通过作垂线AB并找到垂足C与B、D的关系，可以深入探讨此切线的性质。具体来说，若要证明PB为切线，只需连接OA并证明∠PBO=90°。若tan∠ABE=1/2，进一步求sin∠E的值则可以通过相似三角形的关系得出。

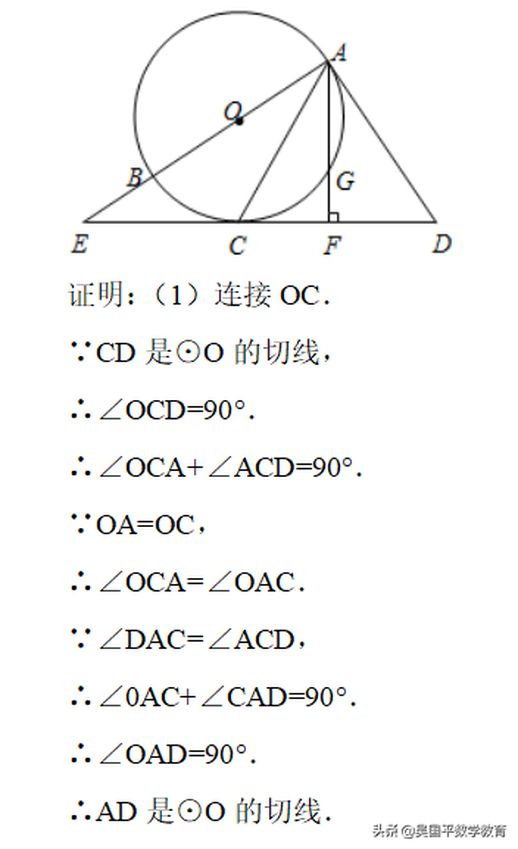
在分析过程中，切线的性质、相似三角形的判定以及三角函数的定义都是必须掌握的要点。例如，在另一个问题中，AB为⊙O的直径，而CD为⊙O的切线。通过连接OC并证明OA与AD的垂直性，可以得出AD为切线的结论。如果给定圆的半径为6cm，EC为8cm，则可以运用勾股定理和相似三角形的性质，逐步求得GF的长度。

进一步分析另一个实例，当AB为⊙O的直径，且CD为过点C的切线时，利用平分线的性质与三角形相似，可以证明AC平分∠DAB。对于复杂的作图问题，可以通过构造和运用几何关系，准确地求出垂线段OE的长度。

直线与圆的关系不仅是几何的基本内容，更是学生理解和应用数学的重要基础。通过深入的练习和分析，学生可以逐步掌握这些知识点，为日后的学习打下坚实的基础。

在学习直线与圆的关系时，切线的判定和性质常常成为考查的重点。切线与半径的垂直关系是理解这一概念的基础。在实际解题过程中，运用图形的辅助线以及已知条件，将复杂的几何关系简化为可处理的数学表达式是关键。例如，在解决与切线相关的问题时，可以通过建立辅助线来分析直线与圆的交点，从而更清晰地认识到切线的性质。

考虑另一个例子，在圆⊙O中，直径AB与切线CD的关系可以通过构造角平分线来探讨。当连接OC并利用切线的性质，能够证明AD是切线。进一步利用勾股定理，可以计算出AE的长度，再通过相似三角形求解出GF的具体数值。这种层层递进的逻辑思维是学生在解题时必须掌握的。

圆周角定理也在这一过程中起到了不可或缺的作用。通过对直径与切线形成的角进行分析，可以引导学生更好地理解角的关系。结合相似三角形的性质，可以将问题转换为已知边长的几何题，从而得出更为直观的解答。重要的是，培养学生对图形的直观理解能力，让他们在复杂的几何问题中找到解决的突破口。

在面对综合性问题时，学生往往需要整合多种知识点来达到最终的解决方案。例如，结合切线、相似三角形和圆周角定理，通过对不同几何元素的相互作用进行分析，能够帮助他们更好地掌握这些知识的内在联系。每一个题目都是一个深入思考的机会，激发学生在数学探索中不断前行。

切线和圆之间的关系不仅仅是一项技能，更是学生思维方式的培养。通过这些例题的学习与解答，学生不仅能掌握直线与圆的基本性质，还能够提高逻辑推理能力和空间想象力。扎实的基础知识是进一步学习高阶数学的关键，帮助学生在今后的数学学习中取得优异的成绩。